CodeForce刷题表

Day4

1604B - XOR Specia-LIS-t

题意:

给定序列a，你可以把它分成若干份，对于每一份，定义hk的值为该部分序列的最长上升子序列的长度，求是否存在一种分割序列a的方法，使h1,h2,…,hk 的异或和为0

思路：

要想异或和为0，就需要二进制的每一位上的1都是偶数个。

进一步想：如果n是偶数，那么直接全部都为1，就可以得到偶数个1，异或和为0

如果n是奇数，那么只要存在一个a[i-1]>=a[i]就可以把这两个合并为1，同样是偶数个1，异或和为0

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+5;
const ll mod = 1e9+7;
int a[N];
int main() {
	int t;
	cin>>t;
	while(t--) {
		int n;
		bool k=0;
		cin>>n;
		for(int i=1;i<=n;i++)
			cin>>a[i];
		if(n&1) {
			for(int i=2;i<=n;i++)
				if(a[i]<=a[i-1])
					k=1;
		}
		else
			k=1;
		if(k)
			cout<<"YES";
		else
			cout<<"NO";
		cout<<endl;
	} 
}

总结：

还是之前总结的，做位运算的题首先把数变成二进制来把握，找到规律以后再进一步思考

1604C - Di-visible Confusion

题意：

一个长为n的数组a1,a2,…,an ，如果在1≤i≤|a|(a当前的长度)存在ai不能被i+1整除则可以删除ai ，剩下的数组变为a1,a2,an-1 。求是否能使数组清空。

思路：

把ai 可能在的位置都遍历一遍(1 ~ i)，如果某一位置可以移除那么他就可以消除，否则永远无法清除。

也就是遍历在 2到i+1的范围内有没有 a[i]的因子！

为什么可以呢？因为每次倒着删一个满足条件的，一直反复操作就会完全清空，由于每次都是从后往前操作不会影响到前面的数，总有一次会删除掉。

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+5;
const ll mod = 1e9+7; 
int a[N];
bool solve() {
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	bool res = false;
	for(int i=1;i<=n;i++) {
		bool k = false;
		for(int j=2;j<=i+1;j++) {
			if(a[i] % j) {
				k = true;
				break;
			}
		}
		if(k == false) 
			return false;
	}
	return true;
}
int main(){
	int _;cin>>_;
	while(_--) {
		if(solve())
			cout<<"YES"<<endl;
		else
			cout<<"NO"<<endl;
	}
	return 0;
}

总结：

会发生变化的数组，不妨从后往前想一想，不要总是从前往后思考。因为从后往前不会对前面的造成影响。

1604D - Moderate Modular Mode

题意：

给定x,y求一个n可以使 n mod x = y mod n

思路：

n%x=y%n , 优先考虑结果为特殊值,如0和y.
n%x=y%n=0,当x=y时,n取x成立,即
n%x=y%n=y,当x>y时,n取x+y成立.

接下来考虑x<y的情况:
这题有两个结论:

  1. n不能<x:
    否则n%x=n,此时y%n=n不可能成立.
  2. n不能>y:
    否则y%n=y,此时n%x=y,那么一定有x>y,与当前条件冲突.
    综上:n在x和y之间.

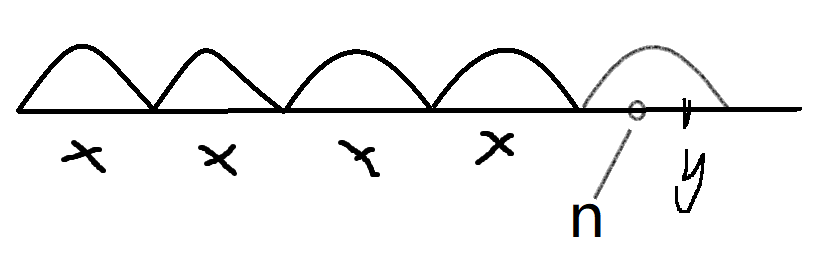
画图:
0开始以步长x开始跳,但不跳过y,设最后的位置为p.
要使得n%x=y%n,取n为p和y的中点即可.

CodeForce - Day4 - 1

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+5;
const ll mod = 1e9+7; 
int main(){
	int _;cin>>_;
	while(_--) {
		ll x,y;
		cin>>x>>y;
		if(x>y)
			cout<<x+y;
		else
			cout<<y-y%x/2;
		cout<<endl;
	}
	return 0;
}

总结：

数论题，优先考虑特殊值，如本题的0和y，然后再找隐藏的式子成立的条件。