最短路问题
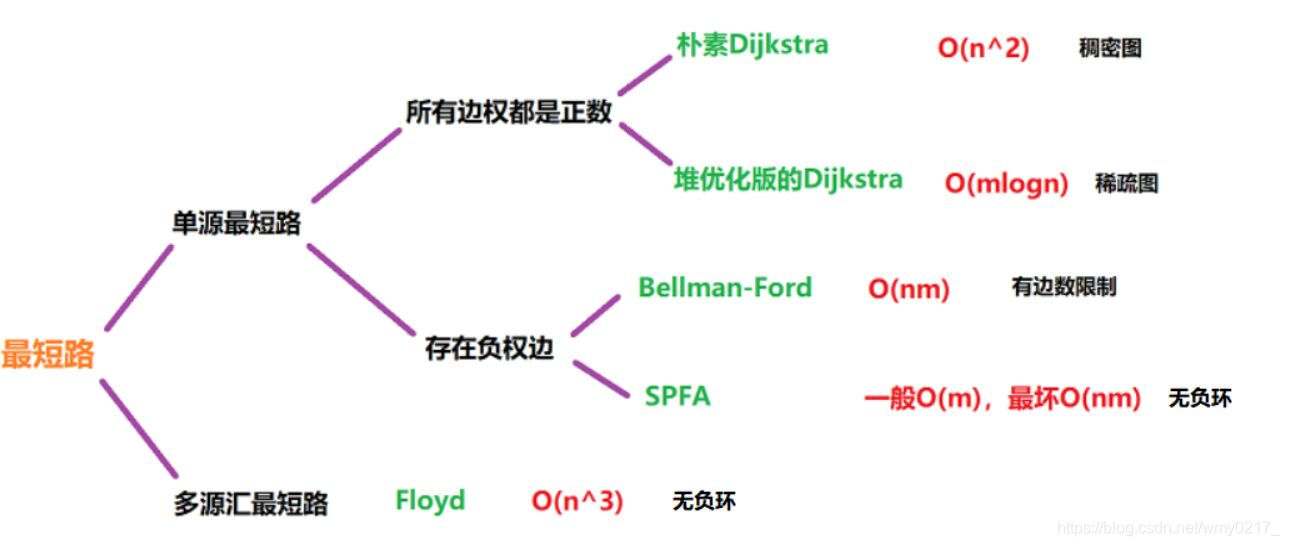
单源最短路:求一个点(dist[1])到其他点的最短路
多源最短路:求任意两个点之间的最短路
稠密图->邻接矩阵存储 m和n^2一个级别
稀疏图->邻接表存储 m和n一个级别
1 . 迪杰斯特拉(Dijkstra)

CODE:
1 | 代码: |
dist[i]存储的是 某个位置(一般是dist[1])到位置i所需要的最短距离
link[i] [j]存储的是 位置i到位置j的距离(注意有向图还是无向图)
k[i]用来标记是否已经使用了该位置。
1的初始位置设为0,其他设为∞.
解析
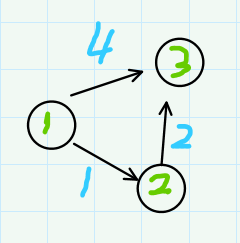
如果是这样的情况找到的第一个t就是位置1(其他的最初都是∞,位置1就是最小的)
首先从位置1试探从位置1到位置2 dist[2]=1 ,从位置1到位置3 dist[3]=4
第二次找到的t是位置2
然后从位置2试探,发现经过位置2到位置3总距离 < 直接从位置1到位置3
即dist[2] + link[2] [3] < dist[3] 所以把 dist[3]修改为3.
最后找到的t是位置3
3不能到达任何位置 结束。
那么为什么要找距离起点最近的点,而不按照顺序来找?
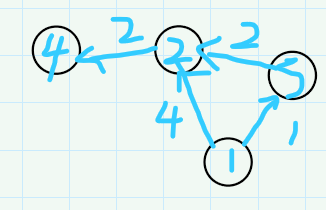
这样的话,如果按照1,2,3,4的顺序来操作就会导致操作时该位置的dist不是最优的,所以该位置对其他位置的操作得到的dist也不是最优的。(从1到2最优的做法是 1->3->2 而不是 1->2,很明显后者比前者多走了1单位距离,那么得到的dist[4]也会相应的多走了一个单位)
由此我们可知我们必须要找到某个位置最优的dist之后才可以使用该点操作。
为什么已经操作过的位置不需要再次操作?
如果一个位置已经操作过了,说明他已经得到了最优的dist。
因为按照之前那个问题,找到的都是距离起点最近的点
那么在这个点之后找到的点都不可能影响到该点最优的dist。
在一个位置修改的位置只可能大于他本身的位置dist[t] + dist[t][i] > dist[t]
所以说,当你找到这个点的时候他就已经是经历过操作的最优的情况了,在他之后的dist只会大于它。
Dijkstra算法为什么不能用于有负边权的图?
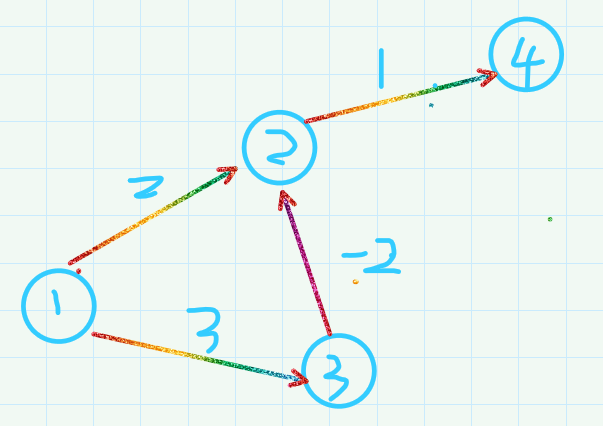
因为Dijkstra算法是通过当前离起点最近的点来更新其他的点的距离,例如上图中的 4 号结点会被 2 号结点更新为2+1=3
但实际上4号结点的最短路径是3+(-2)=1,这样你就知道为什么Dijkstra算法不能用于有负权的边的图吧。


