拓扑排序

什么是拓扑排序？

一个有向无环图(DAG)中，把入度为0的节点输出，直到所有的节点都输出，所输出的序列就是拓扑排序的序列。

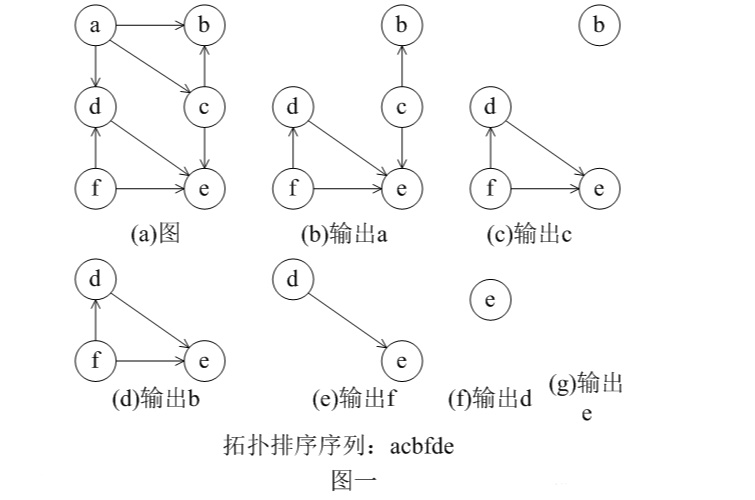
拓扑排序示意图.jpg

如上图所示，a的入度为0输出a，c的入度为0输出c ……最终得到的序列就是acbfde

当然，由于在同一时间可能有多个节点的入度为0，那么拓扑排序所得的序列就不是唯一的，而让他变成唯一的可能就是用到拓扑排序的题的精髓所在(如：字典序，倒序，数小优先 等等……)

举一个生活上的例子：小明是体育委员，他想给同学们按照身高来排队，他每次只能对比两个同学的身高，经过两个两个人的比较，最终就可以得到排好的队伍(由部分的对比来完成整体的对比)

拓扑排序的朴素写法

CODE：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int a[N];//入度值
bool pos[N][N]; //边
int main(){	
    int n,m,x,y,tmp;
    cin>>n>>m;//n个人，m对关系
    for(int i=1;i<=m;i++) {
        cin>>x>>y;
        if(pos[x][y]==false) {
            pos[x][y] = true; //从x可以到达y 
            a[y]++; //y入度+1 
        }
    }
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=n;j++) {//遍历入度为0的节点
            if(a[j]==0) {
                cout<<j<<" "; //输出序列，也可以用数组/vector保存
                a[j]--;
                tmp = j;
                break;
            }
        }
        for(int j=1;j<=n;j++) 
            if(pos[tmp][j])
                a[j]--;
    }
	return 0;
}

解释：

很容易就能想到朴素写法，就是不断的遍历节点，直到所有节点都输出了(注意如果有重复输入的关系，可能需要加一点东西)。

朴素的写法的复杂度是O(n^2)。很容易看出来，确实好写，大多数情况感觉用不到。。

优化版的写法

CODE：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
queue<int> q;
vector<int> edge[n];
for(int i=1;i<=n;i++)  //n  节点的总数
    if(in[i]==0) 
        q.push(i);  //将入度为0的点入队列
vector<int> res;   //res 为拓扑序列
while(!q.empty())
{
    int tmp=q.front(); q.pop(); // 选一个入度为0的点，出队列
    res.push_back(tmp);
    for(int i=0;i<edge[tmp].size();i++)
    {
        int x=edge[p][i];
        in[x]--;
        if(in[x]==0)
            q.push(x);  
    }
}
if(res.size()==n)   
{
    for(int i=0;i<res.size();i++)
        printf( "%d ",res[i] );
    printf("\n");
}
else printf("No Answer!\n");   //  ans 中的长度与n不相等，就说明无拓扑序列

解释：

这样的复杂度是O(n+m)点和边的和，这样就是把每次用n来遍历一个节点换成用队列来遍历，这样的话减完以后变成0的节点直接放在队伍后面就可以了，那么实际上就会跑节点数量和边的数量的和！

欧拉回路

什么是欧拉通路/路径 和 欧拉回路？

欧拉通路:通过图中每条边且只通过一次，并且经过每一个顶点的通路

欧拉回路:通过图中每条边且只通过一次，并且经过每一个顶点回到起始点

无向图如何判断欧拉通路/欧拉回路？

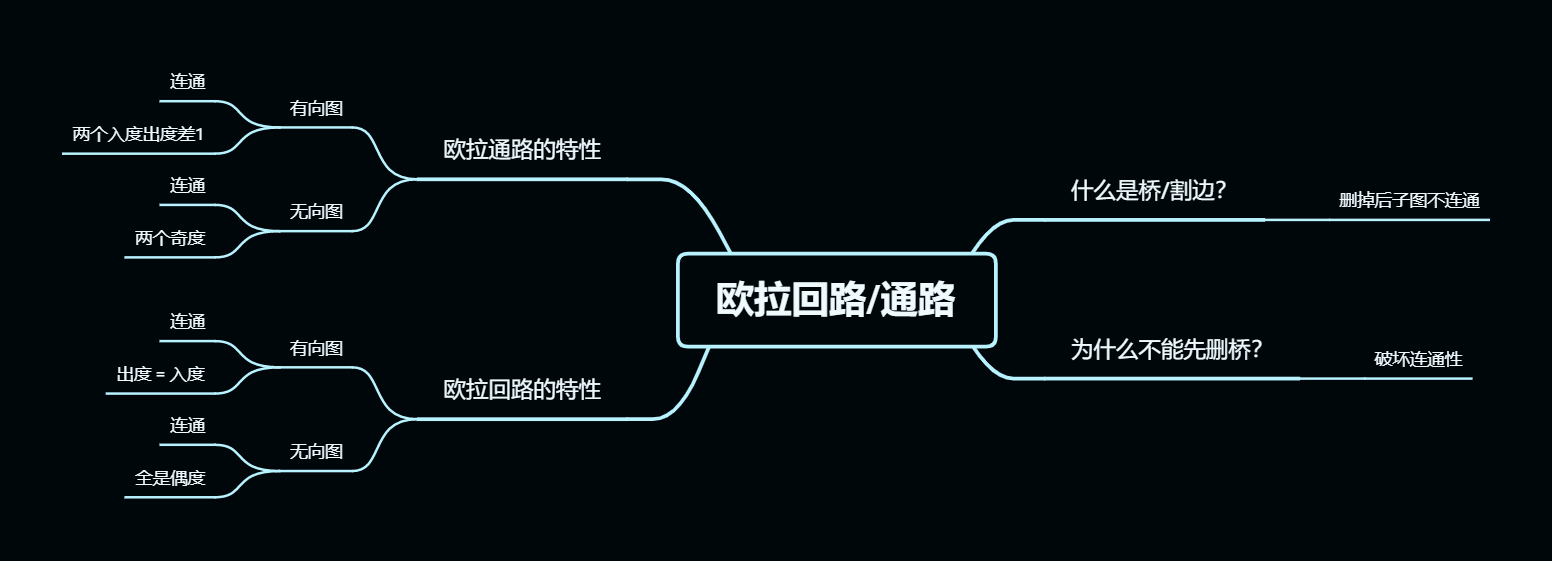
欧拉通路:图连通；图中只有2个度为奇数的节点(就是欧拉通路的2个端点)

欧拉回路:图连通；图中所有节点度均为偶数

有向图如何判断欧拉通路/欧拉回路？

欧拉通路:图连通；除2个端点外其余节点入度=出度；1个端点入度比出度大1；一个端点入度比出度小1

欧拉回路:图连通；所有节点入度=出度

通路.png

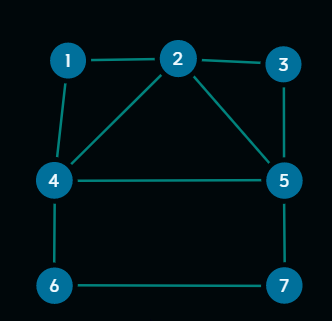
哥尼斯堡七桥问题

18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来（如概述图）。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。

Fleury（佛罗莱）算法

设G 为一无向欧拉图，求G 中一条欧拉回路的算法为：

  1. 任取G 中一顶点v0，令P0 = v0；
  2. 假设沿Pi = v0e1v1e2v2 …eivi 走到顶点vi，按下面方法从E(G) - { e1, e2, …, ei }中选ei+1：
    a) ei+1 与vi 相关联；
    b) 除非无别的边可供选择，否则ei+1 不应该是Gi = G - { e1, e2, …, ei }中的桥。
  3. 当2)不能再进行时算法停止。
    可以证明的是，当算法停止时，所得到的简单回路Pm = v0e1v1e2v2 …emvm, (vm = v0)为G 中一条
    欧拉回路。

欧拉回路桥示例.png

CODE：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
stack<int> st;
int e[100][100],n;
void dfs(int x)
{
    st.push(x);
    for(int i=0;i<n;i++)
        if(e[i][x]>0)
        {
            e[i][x]=e[x][i]=0;  //删除这条边
            dfs(i);
            break;
        }
    return;
}
void fleury(int x)
{
    int flag,u;
    st.push(x);
    while(!st.empty())
    {
        flag=0;
        u = st.top();
        st.pop();
        for(int i=0;i<n;i++)
            if(e[u][i]>0)
            {
                flag=1;
                break;
            }
        if(!flag) 
			printf("%d ",u+1);
        else 
			dfs(u);
    }
    putchar('\n');
}
int main( )
{
    int i,j,u,v,m,degree,num=0,start=0;
    scanf("%d%d",&n,&m);
    for(i=0;i<m;i++)
    {
        scanf("%d%d",&u,&v);
        e[u-1][v-1]=e[v-1][u-1]=1;
    }
    for(i=0;i<n;i++)
    {
        degree=0;
        for(j=0;j<n;j++)
            degree+=e[i][j];
        if(degree&1)
        {
            start=i;
            num++;
        }
    }
    if(num==0||num==2) 
		fleury(start);
    else
		printf("No Euler path\n");
    return 0;
}